Suchfunktion
Förderschwerpunkt Geistige Entwicklung
Mathematik
1 Leitgedanken zum Kompetenzerwerb
1.1 Bildungsgehalt des Faches Mathematik
Durch den Erwerb mathematischer Kompetenzen werden die Schülerinnen und Schüler befähigt, die Welt zu ordnen, zu strukturieren und zu messen. Es ist davon auszugehen, dass die Entwicklung mathematischer Kompetenzen bei allen Kindern in ähnlicher Weise verläuft, auch wenn der Erwerb mathematischer Kompetenzen bei Schülerinnen und Schülern im Förderschwerpunkt geistige Entwicklung eindeutig mehr Zeit benötigt und sich individuell in Qualität und Quantität (auch begrenzt) entwickelt.
Das Fach Mathematik umfasst Inhalte und Verfahren, die räumliche und zeitliche Orientierung und Planung ermöglichen sowie Merkmale, Lebensumstände und Besitzverhältnisse bestimmbar machen. Bereits vor Eintritt in die Schule machen Kinder vielfältige Erfahrungen mit Mustern, Formen, Mengen, Zahlen und Größen bei der Erkundung ihrer Umwelt. Sie vergleichen, unterscheiden, ordnen, klassifizieren und (be-)urteilen. Dabei entwickeln sich parallel zueinander numerische und nicht-numerische Denkstrukturen, die sich wechselseitig beeinflussen.
Mathematik hilft, Geschehnisse wahrzunehmen, zu regulieren, transparent zu machen und mitzugestalten. Sie ermöglicht es, Eindrücke und Urteile durch Quantifizierung, Vergleich und Dokumentation zu überprüfen. Das Fach Mathematik bietet Lösungshilfen und Strategien für Probleme und Aufgaben, an deren Lösung die Schülerinnen und Schüler selbst ein Interesse haben. Problemlösen, Argumentieren und Beweisen, möglichst genaue und angemessene Bezeichnungen, vernetztes Lernen und mathematische Darstellungsformen stellen dabei allgemeine Orientierungen dar. Die Verwendung von Zahlen, der Umgang mit räumlichen und zeitlichen Strukturen (Größen) und Modellbildungen (Darstellungsformen, Wahrscheinlichkeiten, Relationen, Tabellen, Matrizen, Pläne) tragen dazu bei, die eigene Lage, Situationen und erlebte Verhältnisse wahrzunehmen, zu verstehen und sich in ihnen zu orientieren.
Muster und Strukturen sind das Fundament der Mathematik und ziehen sich durch alle Inhaltsbereiche. Das Denken in Mustern und Strukturen macht Denkprozesse ökonomischer und übertragbarer. Wissenselemente und Fertigkeiten können so vernetzt und angewandt werden. Das Wissen um Muster und Strukturen ist für die selbstständige Lösung von mathematischen Fragestellungen von großer Bedeutung.
Mathematik wird so zum Handwerkszeug, mit dessen Hilfe reale Frage- und Problemstellungen gelöst werden können, und leistet damit einen wesentlichen Beitrag zu einem möglichst hohen Maß an Aktivität und Teilhabe am gesellschaftlichen Leben.
Eine zentrale Aufgabe des Mathematikunterrichts ist es, die Schülerinnen und Schüler für den mathematischen Gehalt alltäglicher Situationen und Phänomene zu sensibilisieren und sie zum Problemlösen mit mathematischen Mitteln anzuleiten. In der Auseinandersetzung mit Fragen und Problemen aus ihrer Lebenswelt, aber auch mit konstruierten Sachsituationen erwerben die Schülerinnen und Schüler mathematische Kompetenzen und lernen, diese zu nutzen. Neben dieser Anwendungsorientierung ist es auch Aufgabe des Mathematikunterrichts, den Schülerinnen und Schülern zu ermöglichen, mathematische Muster, Strukturen und Zusammenhänge zu entdecken, diese zu untersuchen und zu nutzen (Strukturorientierung).
Der Mathematikunterricht ist im Sinne der individuellen Lern- und Entwicklungsbegleitung (ILEB) grundsätzlich orientiert an der Lernausgangslage der einzelnen Schülerin beziehungsweise des einzelnen Schülers und greift die unterschiedlichen Alltagserfahrungen und Vorkenntnisse auf, stabilisiert, erweitert und systematisiert sie, um eine breite Ausgangsbasis für die Entwicklung grundlegender mathematischer Kompetenzen aufzubauen. Auf diese Weise wird die Grundlage für das weitere schulische Mathematiklernen und für eine lebenslange Auseinandersetzung mit mathematischen Anforderungen des täglichen Lebens geschaffen.
Die Bereiche Zahlen und Operationen, Raum und Form, Größen und Messen sowie Daten, Häufigkeit und Wahrscheinlichkeit lassen sich nicht nur hierarchisch im Sinne eines entwicklungslogischen Nacheinanders anordnen; sie sind gleich bedeutsam und konstituieren als Gesamtheit das Fach Mathematik.
Basale mathematische Lernfelder (zum Beispiel Raumlage oder Unterschiede wahrnehmen) lassen sich nicht nur dem Fach Mathematik zuordnen, sondern bilden ebenfalls Grundlagen für den Erwerb von Kompetenzen in anderen Fächern.
Mathematik steht in einem wechselseitigen Zusammenhang mit anderen Fächern. Einerseits liefert Mathematik Werkzeuge zur Klärung von Fragen und Problemstellungen der Fächer. Andererseits können Sachsituationen, beispielsweise im Zusammenhang mit den Lebensfeldern, den Ausgangspunkt für Lernprozesse liefern. So können mathematische Begriffe in besonderer Weise veranschaulicht werden und als Feld für vielfältiges Üben dienen. Außerschulische Lernorte bieten Gelegenheiten, Impulse für eine lebensnahe Gestaltung des Mathematikunterrichts aufzunehmen.
Sprache bildet eine zentrale Grundlage für das Erlernen, Verstehen und Vermitteln mathematischer Inhalte.
Beitrag des Faches zu den Lebensfeldern
Der Kompetenzerwerb im Fach Mathematik ist in Verbindung mit der Lebenswelt der Schülerinnen und Schüler zu sehen. Lernfelder ergeben sich aus den Kreuzungspunkten von Lebensfeldern und fachlichen mathematischen Fragestellungen.
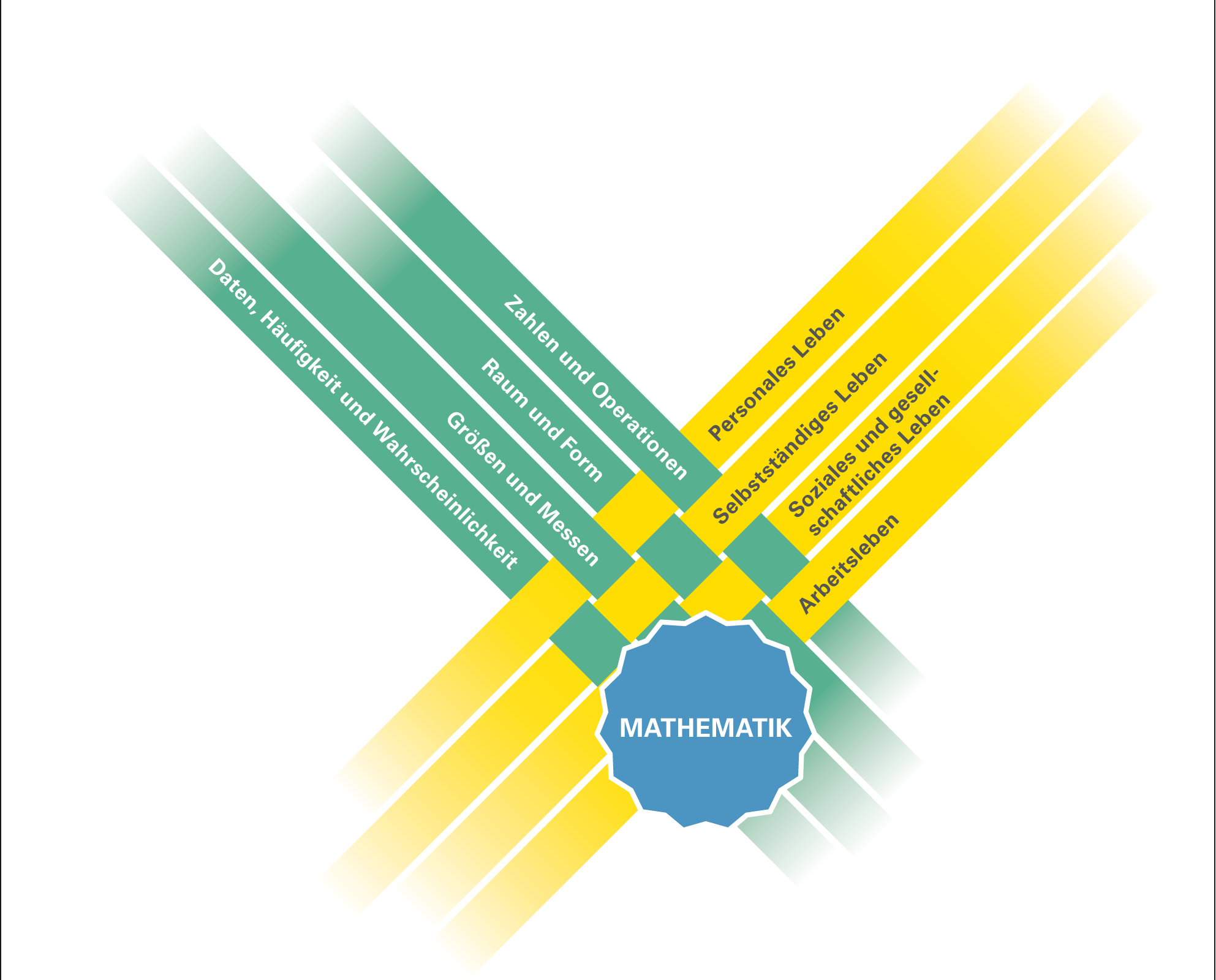
Abbildung 1: Verflechtung Lebensfelder – Mathematik (© Zentrum für Schulqualität und Lehrerbildung Baden-Württemberg)
1.2 Kompetenzen
1.2.1 Inhaltsbezogene Kompetenzen
Die inhaltsbezogenen Kompetenzen beziehen sich im Unterricht aufeinander und werden miteinander vernetzt, so dass einem isolierten Wissenserwerb entgegengewirkt wird. Die inhaltsbezogenen Kompetenzen sind von grundlegender fachlicher Bedeutung und können nur im Zusammenwirken mit den prozessbezogenen Kompetenzen erreicht werden.
Frühe mathematische Kompetenzen werden im Folgenden im Arbeitsbereich „Zahlen und Operationen“ gesondert aufgeführt. In den weiteren drei Arbeitsbereichen werden die frühen mathematischen Kompetenzen in den ausdifferenzierten fachlichen Fragestellungen inhaltlich beschrieben.
Zahlen und Operationen
- Frühe mathematische Kompetenzen
- Zahldarstellung, Zahlaspekte und Zahlbeziehungen verstehen
- Rechenoperationen verstehen und beherrschen
- In Kontexten rechnen
Raum und Form
- Orientierung im Raum
- Wege und Orientierung
- Geometrische Formen und Abbildungen
- Geometrische Körper
Größen und Messen
- Mit Geld umgehen
- Längen, Fläche, Volumen
- Temperatur
- Gewicht
- Zeitliche Orientierung
Daten, Häufigkeit und Wahrscheinlichkeit – Daten erfassen und darstellen
1.2.2 Prozessbezogene Kompetenzen
Für ein erfolgreiches Mathematiklernen mit dem Ziel, Verständnis für mathematische Inhalte aufzubauen, sind die prozessbezogenen mathematischen Kompetenzen von zentraler Bedeutung. Sie verdeutlichen, dass mathematische Grundbildung die Aneignung von Wissen und Fertigkeiten wie auch die Art und Weise der Auseinandersetzung mit Mathematik umfasst. Die Entwicklung einer mathematischen Grundbildung hängt nicht nur von den Unterrichtsinhalten, sondern auch davon ab, in welchem Maße die Schülerinnen und Schüler Gelegenheit bekommen, selbst Probleme mit und ohne Anwendungsbezug zu lösen, eigene Lösungswege zu beschreiben, Begründungen für mathematische Gesetzmäßigkeiten zu finden oder geeignete Darstellungen beim Problemlösen zu entwickeln. Je besser es gelingt, den Mathematikunterricht an den prozessbezogenen mathematischen Kompetenzen auszurichten, desto eher lassen sich positive Einstellungen zur Mathematik aufbauen und Freude an mathematischem Tun fördern.
Dabei sind folgende prozessbezogene Kompetenzen für den Mathematikunterricht wichtig:
Kommunizieren
Kommunikation über mathematische Inhalte erfolgt in kooperativen und interaktiven Unterrichtsprozessen. Die Schülerinnen und Schüler benennen hierbei grundlegende Fachbegriffe, artikulieren eigene Vorstellungen und Ideen und teilen anderen eigene Gedanken mit. Der Mathematikunterricht schafft stetig Situationen, in denen Möglichkeiten zu einer konstruktiven kommunikativen Auseinandersetzung mit mathematischen Sachverhalten gegeben sind. Für nicht oder wenig sprechende Schülerinnen und Schüler werden Möglichkeiten im Sinne der Unterstützten Kommunikation genutzt, damit sie sich entsprechend ausdrücken und beteiligen können.
Argumentieren
Die Schülerinnen und Schüler gewinnen zunehmend Sicherheit, um mathematische Aussagen sprachlich zu fassen, Vermutungen anzustellen, Lösungswege zu begründen und zu diskutieren und verschiedene Standpunkte einzubringen. In kooperativen Arbeitsformen und im Klassengespräch werden soziales und vertiefendes kognitives Lernen gefördert. Auch hier werden alle für die Schülerinnen und Schüler hilfreichen Formen der Kommunikation genutzt.
Problemlösen
Problemlösen meint, dass der Lösungsansatz bei einem mathematischen Problem für die Schülerinnen und Schüler nicht unmittelbar offensichtlich sein kann oder ihnen Lösungsverfahren noch nicht zur Verfügung stehen können. Die Schülerinnen und Schüler entwickeln die Bereitschaft und die Fähigkeit, Probleme zu erfassen, zu beschreiben, unterschiedliche Wege der Problemlösung zu entdecken und zu nutzen. Hierbei sind vielfältige, kleinschrittige und anschauliche Zugänge erforderlich.
Modellieren
Modellieren ist das Bindeglied zwischen Umwelt (ökologische und gesellschaftliche Dimension) und Mathematik. Es umfasst das Strukturieren, Vereinfachen und Übersetzen eines Sachverhalts oder Problems aus der Umwelt in eine mathematische Struktur (Mathematisieren), das Bearbeiten des Problems innerhalb der mathematischen Struktur (im Modell arbeiten), das Übertragen der Lösung auf das reale Problem (Interpretieren) und das Prüfen der Angemessenheit dieser Lösung für das ursprüngliche Problem (Validieren). Dies ist ein oft schwieriger und für die Schülerinnen und Schüler nur schwer nachvollziehbarer Prozess. Der Schwerpunkt hierbei liegt immer auf der Umsetzbarkeit und der Nutzbarkeit für reale Fragestellungen aus der Umwelt.
Darstellen
Die Schülerinnen und Schüler sollen Vorgehensweisen und Arbeitsergebnisse darstellen und dokumentieren können. Sie präsentieren dabei ihre Ideen, Lösungswege und Ergebnisse und tauschen sich darüber aus. Hierbei verwenden sie zunehmend Fachbegriffe und mathematische Zeichen. In gemeinsamer Reflexion lernen sie, verschiedene Darstellungen zu vergleichen und zu bewerten.
1.3 Didaktische Hinweise
Die Schülerinnen und Schüler lernen dann erfolgreich, wenn sie sich ihr mathematisches Wissen aktiv, selbsttätig und kooperativ erarbeiten sowie an ihr bisheriges Wissen anschließen können. Durch diese Selbsttätigkeit und die handlungsorientierte Vorgehensweise wird Mathematik für die Schülerinnen und Schüler nutzbar. Dabei werden auch die Schülerinnen und Schüler in den Blick genommen, die wenig Selbstvertrauen im Fach Mathematik haben, indem positive, sinnstiftende Erlebnisse und Begegnungen mit Mathematik geschaffen werden und ein positives Selbstkonzept gefördert wird.
Regelmäßige diagnostische Prozesse im Rahmen der individuellen Lern- und Entwicklungsbegleitung (ILEB) ermöglichen es, die verschiedenen Kompetenzen in einem Themenbereich festzustellen und nächste Lernziele zu vereinbaren. Dabei werden für die Schülerinnen und Schüler mit einem Anspruch auf ein sonderpädagogisches Bildungsangebot im Förderschwerpunkt geistige Entwicklung auch frühe mathematische Kompetenzen des Faches Mathematik regelmäßig zum Thema gemacht.
Um Unterricht somit möglichst individuell und kompetenzorientiert gestalten zu können, werden die nachfolgenden Unterrichtsprinzipien berücksichtigt:
Muster und Strukturen
Muster und Strukturen sind ein übergreifendes Prinzip in der Mathematik. Bei allen inhaltlichen Themen ist es von großer Bedeutung, dass die Auseinandersetzung mit den zugrundeliegenden Mustern und Strukturen ermöglicht wird, Verstehensprozesse unterstützt werden, damit Schülerinnen und Schüler beim Lösen von Fragestellungen darauf zurückgreifen können.
Zahlen von Anfang an
Die Entwicklungslogik der Mathematik ist nicht streng hierarchisch, sondern verläuft in vielen Bereichen parallel und vernetzt. Eine Unterteilung in „pränumerische“ und numerische Inhalte ist nicht zielführend. Klassifikationsübungen eignen sich beispielsweise zur Bildung von Oberbegriffen, aber nur in Verbindung mit Mengen und Zahlen können mathematische Kompetenzen (numerische und nicht-numerische) erworben werden. In diesem Zusammenhang sind das Zählen und alle damit verbundenen Kompetenzen von großer Bedeutung.
Lebensweltbezug
Mathematikunterricht geht – wo immer möglich – von realen Situationen aus dem Schulleben, der Umwelt und dem Alltag aus. Gerade solche Situationen, zu denen bei Schülerinnen und Schülern auch das Spiel zählt, bieten reiche und sinnvolle Möglichkeiten für Mathematisierungsprozesse. Zu erwerbende Kompetenzen sollen Schülerinnen und Schüler zu einer Erschließung von Welt und Lösung von realen Problem- und Fragestellungen befähigen und somit eine gegenwärtige oder zukünftige Bedeutung aufweisen.
Aktiv-entdeckendes Lernen
Entdeckendes Lernen weckt Neugier, fordert Kreativität und Anstrengungsbereitschaft heraus. Die Schülerinnen und Schüler können vor allem dann individuelle Lösungsansätze und Strategien entwickeln sowie mathematische Strukturen und Gesetzmäßigkeiten entdecken, wenn sie mit herausfordernden Fragestellungen in offenen Aufgaben konfrontiert werden. Der Unterricht schafft deshalb den Rahmen für aktiv-entdeckendes Lernen.
Orientierung an der Entwicklung und am Lebensalter
Die Lernangebote sind orientiert am Entwicklungsstand im Bereich Mathematik und am Lebensalter der Schülerinnen und Schüler. Hierzu bedarf es einer präzisen Diagnostik im Hinblick auf den mathematischen Entwicklungsstand und die Berücksichtigung des Alters, der Lebenserfahrung und des Interesses der einzelnen Schülerin und des einzelnen Schülers. Dabei ist zu beachten, dass die Schülerinnen und Schüler im Förderschwerpunkt geistige Entwicklung sehr unterschiedliche Formen finden und entwickeln, um die Welt zu erleben und sich aktiv anzueignen.
Handlungsorientierung
Handlungsorientiertes Lernen ist Voraussetzung für verstehenden Mathematikunterricht. Durch ein Zusammenspiel von Orientieren, Planen, Durchführen und Reflektieren entstehen Denkstrukturen. Handlungsorientierung ermöglicht jeder Schülerin und jedem Schüler, auf seiner Stufe des Könnens zu arbeiten. Wahrnehmungserfahrungen, Handlungsmöglichkeiten und geeignete Veranschaulichungen dienen auch dazu, mathematische Muster und Strukturen zu erkennen und das Verständnis insbesondere für Zahlen und Rechenoperationen zu festigen und zu stabilisieren. Sprachliche Beschreibungen des Vorgehens unterstützen dabei den Verstehensprozess.
Ganzheitliches Lernen
Mathematisches Lernen ist ein aktiver, kreativer und individueller Prozess und umfasst weit mehr als das Speichern einzelner Fakten oder Wissensbausteine. Mathematisches Lernen soll – soweit möglich – in sinnvollen Zusammenhängen stattfinden, was nicht ausschließt, dass für das Verstehen des Zusammenhangs auch das Üben einzelner Lerninhalte nötig sein kann.
Mathematik ist wechselseitig mit den Lebensfeldern und anderen Fächern verbunden. Mathematische Begriffe können oft in besonderer Weise veranschaulicht werden und bieten häufig Möglichkeiten für vielfältiges Üben. Für eine lebensnahe Gestaltung des Mathematikunterrichts werden sowohl Fragestellungen aus der aktuellen Lebenswelt der Schülerinnen und Schüler in den Unterricht einbezogen als auch Möglichkeiten gesucht, wie mathematische Inhalte an außerschulischen Lernorten sowie in handlungsorientierten Situationen mit Anwendungsbezug aufgegriffen werden können.
Unterschiedliche Darstellungsformen
Die Entwicklung von Zahl- und Operationsverständnis, von Größenvorstellungen und geometrischen Vorstellungen ist grundlegend für den Erwerb mathematischer Kompetenzen.
Erst auf der Basis gesicherter Vorstellungsbilder kann sich mathematisches Verständnis entwickeln. Hierfür müssen vielfältige Erfahrungs- und Handlungsmöglichkeiten auf unterschiedlichen Abstraktionsniveaus geschaffen und der Wechsel innerhalb und zwischen diesen ermöglicht werden. Sinnliche Erfahrungen, bildliche und modellhafte Darstellungen sind dabei ein wichtiges Bindeglied zwischen Handlungen und dem jeweiligen Arbeitsbereich (Zahlen und Operationen, Raum und Form, Größen und Messen sowie Daten, Häufigkeit und Wahrscheinlichkeit).
Die gewählte Ebene der Darstellung (enaktiv, ikonisch und symbolisch) orientiert sich an den Möglichkeiten und dem Bedarf der Schülerinnen und Schüler. Für den Kompetenzerwerb und für die Entwicklung des mathematischen Verständnisses ist es jedoch entscheidend, dass immer ein Wechsel zwischen den unterschiedlichen Darstellungsebenen stattfindet.
Versprachlichung
Die Versprachlichung von Handlungen, Vorstellungen, Darstellungen, Strukturen und Operationen ist für das Ausprägen von Vorstellungsbildern von großer Bedeutung. Begriffe werden geklärt, verstanden und angemessen angewandt. „Lautes Denken“, das Beschreiben, Aufschreiben und Darstellen von Vorgehensweisen und der Austausch darüber begünstigen durch ihre strukturierende Wirkung Lernprozesse. Dadurch erhalten die Lehrkräfte zusätzlich wertvolle diagnostische Informationen für den kompetenzorientierten Mathematikunterricht. Bei nicht oder wenig sprechenden Schülerinnen und Schülern sind entsprechende Hilfsmittel im Sinne der Unterstützten Kommunikation zu nutzen.
Konstruktive Fehlerkultur
Fehler sind natürliche und notwendige Bestandteile mathematischer Lernprozesse. Sie geben wertvolle Einblicke in die Denkweisen der Schülerinnen und Schüler und sind Anlass zur Reflexion. Die Lehrkräfte sorgen für ein angstfreies Verhältnis der Schülerinnen und Schüler Fehlern gegenüber. Dies setzt voraus, dass auch sie selbst und die Eltern entspannt und konstruktiv mit Fehlern umgehen und diese als Lernchance wahrnehmen und nutzen.
Üben
Üben ist ein wichtiger Bestandteil mathematischen Lernens. In jeder Phase eines Lernprozesses sind Übungen sinnvoll und wichtig. Diese erfolgen nicht nur auf der abstrakt-symbolischen Darstellungsebene, sondern auch in Verbindung zur Handlungs- und Bildebene. Bei der Gestaltung von Übungsphasen ist zu beachten, dass nicht deren quantitative Ausweitung Lernerfolge erzeugt, sondern die Qualität der Übungsaufgaben die Lernprozesse entscheidend beeinflusst. Deshalb werden neben Übungsformen zur Automatisierung auch operative und produktive Übungsformen verwendet, die Entdeckungen ermöglichen und Einsicht in mathematische Muster und Strukturen fördern.
2 Kompetenzfelder
2.1 Grund-, Haupt- und Berufsschulstufe
2.1.1 Zahlen und Operationen
2.1.1.1 Frühe mathematische Kompetenzen
Alle Schülerinnen und Schüler kommen mit mathematischen Vorerfahrungen aus ihrem Alltag in die Schule. Sie erfahren mathematische Operationen beispielsweise der Addition und Subtraktion bereits durch einfache Handlungen wie „etwas wird mehr“ und „etwas wird weniger“. Dadurch entsteht mathematisches Wissen. Der Mathematikunterricht erfordert eine exakte und präzise Lehrersprache, die Handlungen begleitet und dadurch auch zur Anschaulichkeit beiträgt.
Die frühen mathematischen Kompetenzen umfassen gleichwertig sowohl numerische als auch nicht-numerische Inhalte. Dazu gehört die Fähigkeit, Mengen und deren Veränderung zu erfassen, zu vergleichen, zu beschreiben und Einsicht zu gewinnen in die Zerlegbarkeit von Mengen (Teil-Ganzes-Beziehung). Auch das strukturierte Erfassen von Mengen ist in diesem Zusammenhang von Bedeutung. Frühe mathematische Kompetenzen umfassen weiter die Kenntnis von Zahlwörtern und Zahlwortreihen, die Beachtung von Zählstrategien, sowie die Einsicht in grundlegende Konzepte wie Invarianz, Seriation und Eins-zu-Eins-Zuordnung. Eine wichtige Entwicklungsaufgabe im Bereich der frühen mathematischen Kompetenzen ist die Verknüpfung von numerischen und nicht-numerischen Kompetenzen.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.1.2 Zahldarstellungen, Zahlaspekte und Zahlbeziehungen verstehen
Im Alltag erscheinen uns Zahlen unter verschiedenen Aspekten: Sie können die Mächtigkeit von Mengen ausdrücken (zum Beispiel „3 Äpfel“), als Maßzahlen fungieren (zum Beispiel „100 g“) oder die Vielfachheit einer Handlung (zum Beispiel „noch zweimal schlafen“) bezeichnen. Um eine tragfähige Zahlvorstellung zu entwickeln, sollen die Schülerinnen und Schüler zunächst die Zusammenhänge der Zahlen untereinander und die Beziehungen zwischen den Zahlen verstehen können. Das Verständnis für eine kardinale (Zählzahl) und ordinale (Ordnungszahl) Zahlvorstellung und das Erfassen von Zahlbeziehungen ist hier von besonderer Bedeutung. Um bei Zahldarstellungen den Schülerinnen und Schülern die Anzahlerfassung in den Vordergrund zu rücken, werden unterschiedliche Zahldarstellungen im Unterricht verwendet.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.1.3 Rechenoperationen verstehen und beherrschen
Aus alltäglichen Situationen und unterrichtlichen Aufgabenstellungen ergeben sich für die Schülerinnen und Schüler nachvollziehbare Zusammenhänge, Anlässe und Notwendigkeiten, in denen sie Zahlen und Mengen erfassen, vergleichen, zusammenzählen, abziehen, vervielfachen und teilen. Aus dem konkreten Alltagsbezug entstehen Sachrechenaufgaben.
Konkrete anlassbezogene Zugänge werden durch die systematische Erarbeitung ergänzt. Ziffern und Operationszeichen sind diejenigen Grundelemente, mit denen sich Sachverhalte mathematisch darstellen lassen. Es geht um Verfahren und Regeln des Operierens mit Zahlen und deren Anwendung in bedeutsamen Situationen und deren Notation.
Die Schülerinnen und Schüler lernen wichtige mathematische Zeichen, Fachbegriffe, Notationsformen und verwenden diese entsprechend. Dem Üben und Automatisieren von Rechenoperationen (zum Beispiel kleines Eins-plus-Eins, Zahlzerlegungen) kommt in diesem Zusammenhang eine wichtige Bedeutung zu. Bei eingesetztem Material ist immer wieder dessen Notwendigkeit zu hinterfragen, um wann immer möglich eine Loslösung von Material und zählendem Rechnen anzustoßen.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.1.4 In Kontexten rechnen
Die Schülerinnen und Schüler erschließen sich mit mathematischen Mitteln einfache Problemstellungen aus ihrer Lebenswelt.
Indem Rechenoperationen in Kontexten (wenn nötig mit Realgegenständen als Anschauung) eingebettet werden, können die Beziehungen zwischen den vier Grundrechenarten verinnerlicht werden. Um sich in mathematischen Kontexten verständigen zu können, wird ein sicherer Umgang mit Zeichen, Fachbegriffen und Notationsformen gefördert.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.2 Raum und Form
2.1.2.1 Orientierung im Raum
Die Schülerinnen und Schüler lernen Körper-Raum-Verhältnisse wahrzunehmen und zu verändern. Über körperbezogene Zugänge werden räumliche Sachverhalte erfasst. Die den geometrischen Begriffen zugrundeliegenden elementaren Körper-Raum-Verhältnisse werden ihnen in Raum-Lage-Beziehungen verdeutlicht wie auch in den damit korrespondierenden Präpositionen (zum Beispiel vor, hinter, neben, rechts und links, unter, über). Die Erfahrung von Räumen wird im Nacheinander, in der Abfolge von Dingen, Räumen und Stationen konkretisiert. Die eigenen Bewegungs- und Wahrnehmungsmöglichkeiten bilden hierbei die Grundlage und Voraussetzung für den Aufbau geometrischer Begriffe. Die Schülerinnen und Schüler lernen so, sich in den Räumen der Schule zu orientieren und diese mitzugestalten.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.2.2 Wege und Orientierung
Die Schülerinnen und Schüler erweitern ihre Mobilität durch Orientierung an konkreten Orten, einfachen Überblicksdarstellungen und Landkarten. Die Kenntnis von Wegen und Orten ermöglicht und festigt sozialräumliche und geographische Vorstellungen. Das je individuelle Wegekonzept bildet dabei die notwendige planerische Voraussetzung für unterrichtliche Angebote.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.2.3 Geometrische Formen und Abbildungen
Die Schule schafft Angebote, in denen die Schülerinnen und Schüler ihre Kenntnisse über geometrische Sachverhalte einbringen und erweitern können. Geometrische Grundformen bringen Übersicht in eine Situation („Wir stellen uns im Kreis auf“, Warteschlange vor der Kasse). Markierungen einer Aktionsfläche (Sandkasten, Spielfeld) helfen bei der Orientierung („geradeaus, dann nach rechts gehen“) und qualifizieren Dinge und Räume („das fehlende Teil ist rund“). Erworbene Kompetenzen bilden die Grundlage für eine Kompetenzerweiterung im Bereich Dreidimensionalität. Anknüpfend an Alltagsbegriffe entwickelt sich zunehmend eine geometrische Fachsprache.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.2.4 Geometrische Körper
Der handelnde Umgang mit realen Formen ist Voraussetzung für den Aufbau eines räumlichen Vorstellungsvermögens. Mathematisierte Grundformen wie Dreieck, Rechteck, Quadrat und Kreis sind deshalb stets Grundlage. Ihre begriffliche Fassung wird im Konstruktionsspiel ebenso wie in alltäglichen Situationen angebahnt und aufgebaut: Geschlossenheit beziehungsweise Offenheit, Parallelen, Abschnitte, Winkel, Abstände, Strecken und Symmetrien werden anschaulich, sprachlich und konstruktiv dargestellt.
Exaktes Zeichnen, sorgfältiges Konstruieren sowie die sichere Handhabung verschiedener Zeichengeräte werden als Voraussetzungen für weitergehende Erkenntnisse eingesetzt. Das Bauen mit Körpern (zum Beispiel freies Bauen, Nachbauen, Weiterbauen) stellt hierbei die elementare Tätigkeit dar.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
2.1.3 Größen und Messen
2.1.3.1 Mit Geld umgehen
Der Umgang mit Geld ist für die selbstständige Lebensbewältigung beziehungsweise für die gesellschaftliche Teilhabe von großer Bedeutung. Alltagssituationen wie Einkaufen, Umgang mit dem Taschengeld und Verkaufssituationen (etwa Verkauf am Weihnachtsmarkt) bieten lebenspraktische Lernfelder und können Ausgangspunkt für das Rechnen mit Geld sein. Hierbei entwickeln die Schülerinnen und Schüler Größenvorstellungen, die ihnen bei der Strukturierung des Alltags helfen. Geld ist eine Zählgröße und keine physikalische Größe und es gibt auch keine Messgeräte. Dadurch, dass der Preis eines Produktes (zum Beispiel durch Qualität oder Sonderangebote) unterschiedlich ausfallen kann, ist der Aufbau von Stützpunktwissen beziehungsweise die Entwicklung von Stützpunktvorstellungen erschwert.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
2.1.3.2 Längen, Flächen, Volumen
Ausgehend von der Wahrnehmung des eigenen Körpers und der Beziehung zu seiner Umwelt entwickeln die Schülerinnen und Schüler Vorstellungen von räumlicher Ausdehnung und Begrenzung.
Durch den Umgang mit Längen, Flächen und Volumina entwickeln die Schülerinnen und Schüler realistische Größenvorstellungen. Diese Erfahrungen helfen ihnen bei der Bewältigung von alltäglichen Situationen wie dem Lesen von Plänen und dem Abmessen von Zutaten. Diese Kenntnisse und Fähigkeiten können zur Strukturierung und zur selbstständigen Gestaltung des Alltags genutzt werden. Längen, Flächen und Volumen sind visuell wahrnehmbare Größen. Der Aufbau von Stützpunktwissen und Stützpunktvorstellungen durch vielfältige Messerfahrungen ermöglicht es den Schülerinnen und Schülern unter anderem auch, unterschiedliche Schätzaufgaben zu bewältigen, denn Schätzen ist ein gedankliches Vergleichen mit bekannten Größen.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.3.3 Temperatur
Die Schülerinnen und Schüler setzen sich aktiv mit dem Thema Temperatur auseinander. Dies bildet eine wichtige Grundlage für den Kompetenzerwerb in den Bereichen Wetter, Naturphänomene und Selbstversorgung (zum Beispiel im Blick auf Fieber oder Kleidung). Sie dient auch dem Schutz vor gesundheitlichen Risiken. Kenntnisse und Erfahrungen können zur Strukturierung und zur selbstständigen Gestaltung des Alltags genutzt werden. Temperatur ist eine Größe, die gemessen werden kann, aber auch durch unsere Sinnesorgane wahrgenommen und individuell interpretiert wird. Das Schätzen von Temperaturen ist schwierig, da dies von unserem Körper stark beeinflusst wird.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
2.1.3.4 Gewicht
Die Auseinandersetzung mit dem Thema Gewicht stellt für die Schülerinnen und Schüler eine wichtige Grundlage für die Strukturierung und Bewältigung des Alltags dar. Lebenspraktische Bezüge zu den Bereichen Kochen, Gesunderhaltung und Orientierung im Alltag werden im Unterricht genutzt. Dabei können passende Repräsentanten helfen, Stützpunktwissen und Stützpunktvorstellungen aufzubauen. Das Gewicht eines Gegenstandes ist nur bedingt visuell wahrnehmbar, und bei Schätzungen wird häufig die Größe eines Gegenstandes mit dem Gewicht in Verbindung gebracht. Die Schülerinnen und Schüler benötigen daher vielfältige Möglichkeiten, sich handelnd mit verschiedenen Messgeräten auseinanderzusetzen.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
2.1.3.5 Zeitliche Orientierung
Die zeitliche Strukturierung stellt für die Schülerinnen und Schüler eine wichtige Grundlage für die Orientierung im Alltag und für die Teilhabe an der Gesellschaft dar. Lebenspraktische Bezüge ergeben sich beispielsweise im Schulalltag durch die Strukturierung der Tage und Wochen (zum Beispiel im Stundenplan).
Zeit kann man nicht sehen, aber man kann sie messen, objektiv über diese Messung (Zeitpunkte, Zeitspannen) beschreiben und subjektiv wahrnehmen. Ob etwas lang oder kurz dauert, ist individuell und situativ unterschiedlich. Der Aufbau von Stützpunktwissen und Stützpunktvorstellungen bedarf einer intensiven Auseinandersetzung mittels Schätzung und Messung von Zeitspannen.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
2.1.4 Daten, Häufigkeit, Wahrscheinlichkeit – Daten erfassen und darstellen
Die Schülerinnen und Schüler erleben verschieden Anlässe, bei denen Daten, gesammelt und ausgewertet werden. Sie erschließen sich ihre unmittelbare Erfahrungswelt, indem sie Daten sammeln, strukturieren und darstellen. Die Auseinandersetzung mit den hieraus gewonnenen Informationen und Erkenntnissen befähigt die Schülerinnen und Schüler zunehmend, Situationen einzuschätzen und zu bewerten. Hierfür bietet die konkrete Lebens- und Alltagswelt der Schülerinnen und Schüler eine authentische Ausgangslage und regt zu Fragestellungen an. Durch Erfahrungen beispielsweise in Spielsituationen sind Kinder immer wieder mit dem „Zufall“ konfrontiert. Die Frage nach Wahrscheinlichkeiten und Sicherheiten stellt sich auch in der alltäglichen Erfahrungswelt der Schülerinnen und Schüler.
| Denkanstöße | Kompetenzspektrum |
|---|---|
|
Die Schülerinnen und Schüler
|
| Beispielhafte Inhalte | Exemplarische Aneignungs- und Differenzierungsmöglichkeiten |
|
Die Schülerin oder der Schüler
|
| Bezüge und Verweise | |
|
|
3 Anhang
3.1 Verweise
Das Verweissystem im Bildungsplan für Schülerinnen und Schüler mit Anspruch auf ein sonderpädagogisches Bildungsangebot im Förderschwerpunkt Geistige Entwicklung unterscheidet acht verschiedene Verweisarten. Diese werden durch unterschiedliche Symbole gekennzeichnet:
| Bezüge und Verweise |
|---|
|
Im Folgenden wird jeder Verweistyp beispielhaft erläutert:
| Verweise | Erläuterung |
|---|---|
| Verweis auf ein Lebensfeld: Arbeitsleben, Kompetenzfeld 2.1.1 Grundhaltungen und Schlüsselqualifikationen | |
| Verweis auf ein Fach: Bewegung, Spiel und Sport, Kompetenzfeld 2.1.4 Bewegen an Geräten | |
| Verweis auf eine prozessbezogene Kompetenz aus dem Bildungsplan der Grundschule, Fach Deutsch, Bereich 2.1 Sprechen und Zuhören, Teilkompetenz 1 | |
| Verweis auf Standards für inhaltsbezogene Kompetenzen aus dem Bildungsplan der Sekundarstufe I, Fach Musik, Bereich 3.1.3 Musik reflektieren | |
| Verweis auf eine Leitperspektive BNE = Bildung für nachhaltige Entwicklung, zentraler Aspekt Demokratiefähigkeit | |
| Verweis auf den Leitfaden Demokratiebildung, Seite 43 | |
| Verweis auf den Rechtschreibrahmen, Seite 25-30 |
Es wird vorrangig auf den Bildungsplan der Grundschule und der Sekundarstufe I verwiesen. Der Bildungsplan des Gymnasiums ist dabei mitbedacht, aus Gründen der Übersichtlichkeit werden diese Verweise nicht gesondert aufgeführt.
3.2 Abkürzungen
| Lebensfelder des Bildungsplans für Schülerinnen und Schüler mit Anspruch auf ein sonder-pädagogisches Bildungsangebot im Förderschwerpunkt geistige Entwicklung | |
|---|---|
| PER | Personales Leben |
| SEL | Selbstständiges Leben |
| SOZ | Soziales und gesellschaftliches Leben |
| ARB | Arbeitsleben |
| Allgemeine Leitperspektiven | |
|---|---|
| BNE | Bildung für nachhaltige Entwicklung |
| BTV | Bildung für Toleranz und Akzeptanz von Vielfalt |
| PG | Prävention und Gesundheitsförderung |
| Themenspezifische Leitperspektiven | |
| BO | Berufliche Orientierung |
| MB | Medienbildung |
| VB | Verbraucherbildung |
| LFDB | Leitfaden Demokratiebildung |
| Bildungspläne 2016 | |
|---|---|
| GS | Bildungsplan der Grundschule |
| SEK1 | Gemeinsamer Bildungsplan für die Sekundarstufe I |
| GYM | Bildungsplan des Gymnasiums |
| GMSO | Bildungsplan der Oberstufe an Gemeinschaftsschulen |
| Fächer | |
|---|---|
| AES | Alltagskultur, Ernährung und Soziales |
| BMB | Basiskurs Medienbildung |
| BSS | Bewegung, Spiel und Sport |
| BK | Bildende Kunst |
| BIO | Biologie |
| BNT | Biologie, Naturphänomene und Technik |
| CH | Chemie |
| D | Deutsch |
| E | Englisch |
| ETH | Ethik |
| REV | Evangelische Religionslehre |
| F | Französisch |
| GK | Gemeinschaftskunde |
| GEO | Geographie |
| G | Geschichte |
| KUW | Kunst und Werken |
| RRK | Katholische Religionslehre |
| M | Mathematik |
| MFR | Moderne Fremdsprache |
| MUS | Musik |
| NwT | Naturwissenschaft und Technik |
| PH | Physik |
| SU | Sachunterricht |
| SPO | Sport |
| T | Technik |
| WBO | Wirtschaft und Berufsorientierung |
| WBS | Wirtschaft, Berufs- und Studienorientierung |






