Um unsere Webseite für Sie optimal gestalten und verbessern zu können, verwenden wir Cookies.
Weitere Informationen zu Cookies erhalten Sie in unserer Datenschutzerklärung.
1. Leitgedanken zum Kompetenzerwerb
1.1 Bildungswert des Faches Mathematik
Mathematik ist eine zentrale kulturelle und zivilisatorische Errungenschaft. Mathematik unterstützt bei der Bewältigung vielfältiger Lebenssituationen und dient kulturübergreifend als Sprache in einer zunehmend technisierten und ökonomisierten Welt. So zählt beispielsweise mathematische Modellierung zu den basalen Werkzeugen und ihre Ergebnisse sind als Zugang zum Verständnis der Welt und als Orientierung in der Welt von entscheidender Bedeutung. Darüber hinaus ist Mathematik eine eigenständige und lebendige Wissenschaft mit einer deduktiv geordneten Welt eigener Art.
Kompetenzentwicklung
Eine mathematische Grundbildung hat zum Ziel, die Rolle der Mathematik in der Welt zu verdeutlichen und die Schülerinnen und Schüler in die Lage zu versetzen, mathematisches Wissen funktional einzusetzen und in vielfältigen Situationen mathematisch begründet Entscheidungen zu treffen oder Aussagen zu beurteilen. Mathematische Bildung befähigt die Schülerinnen und Schüler, sich in ihrer Lebenswelt zu orientieren, diese auch unter mathematischen Gesichtspunkten zu betrachten und zu verstehen und Mathematik in Beruf und Studium erfolgreich und verantwortlich anzuwenden.
Mathematische Bildung trägt zur Bildung der Schülerinnen und Schüler bei, indem sie ihnen insbesondere folgende Grunderfahrungen nach Winter ermöglicht, die miteinander in engem Zusammenhang stehen:
- technische, natürliche, soziale und kulturelle Erscheinungen und Vorgänge mithilfe der Mathematik wahrnehmen, verstehen und unter Nutzung mathematischer Gesichtspunkte beurteilen;
- Mathematik mit ihrer Sprache, ihren Symbolen, Bildern und Formeln in der Bedeutung für die Beschreibung und Bearbeitung von Aufgaben und Problemen inner- und außerhalb der Mathematik kennen und begreifen;
- in der Bearbeitung von Fragen und Problemen mit mathematischen Mitteln allgemeine Problemlösefähigkeit erwerben.
Entwicklung der Persönlichkeit
Die Beschäftigung mit innermathematischen oder mathematisierbaren Problemen trägt wesentlich zur Entwicklung der Persönlichkeit bei. Leistungsbereitschaft, Konzentrationsfähigkeit, Ausdauer, Sorgfalt, Exaktheit und Zielstrebigkeit werden gefördert und gefordert. Die Schülerinnen und Schüler erkennen, dass zur Bewältigung mathematischer Herausforderungen der Aufbau mathematischen Wissens und präzises Denken und Formulieren notwendig sind. Sie übernehmen Verantwortung für das eigene Lernen, erzielen Erfolgserlebnisse beim mathematischen Arbeiten, sei es allein oder in der Gruppe, und reflektieren eigene Denk- und Lösungsansätze und die anderer. So eröffnet der Mathematikunterricht Chancen zur Entwicklung eines positiven Selbstkonzepts und einer verantwortlichen Selbstregulation.
Beitrag des Faches zu den Leitperspektiven
In welcher Weise das Fach Mathematik einen Beitrag zu den Leitperspektiven leistet, wird im Folgenden dargestellt:
- Bildung für nachhaltige Entwicklung (BNE)
Der Mathematikunterricht trägt dazu bei, dass Kinder und Jugendliche befähigt werden, in vielfältigen Kontexten und Lebensbereichen verantwortungsvoll und nachhaltig zu denken und zu agieren. Als Grundlagenfach leistet Mathematik im Prinzip mit all seinen Kompetenzbereichen Beiträge zur Bildung für nachhaltige Entwicklung, insbesondere im Rahmen der Leitideen Funktionaler Zusammenhang beziehungsweise Daten und Zufall.
Durch entsprechende Themenauswahl bietet der Unterricht Anlass, über gesellschaftliche, wirtschaftliche und wissenschaftliche Zusammenhänge und Entwicklungen nachzudenken. Die Mathematik stellt Werkzeuge zur Verfügung, um bei Fragen nachhaltiger Entwicklung fundierte Aussagen zu treffen und zu sachlich begründeten Bewertungen zu kommen. - Bildung für Toleranz und Akzeptanz von Vielfalt (BTV)
Aus dem Stellenwert des Faches Mathematik erwächst die Verantwortung, im Unterricht seine Bedeutung durch häufigen Bezug zur realen Welt herauszuarbeiten. Mit geeigneten, anwendungsorientierten Aufgaben und durch die Art der Behandlung können Aspekte der Bildung für Toleranz und Akzeptanz von Vielfalt aufgegriffen werden. - Prävention und Gesundheitsförderung (PG)
Mit den Arbeitsweisen und Methoden des Mathematikunterrichts wird ein wesentlicher Beitrag zur Entwicklung der Persönlichkeit im Sinne der Leitperspektive Prävention und Gesundheitsförderung geleistet. Die Schülerinnen und Schüler erwerben durch Beobachtung von modellhaftem Verhalten sowie durch eigene Erfahrungen Lebenskompetenzen vor allem in den Lern- und Handlungsfeldern „Gedanken, Emotionen und Handlungen selbst regulieren“ und „ressourcenorientiert denken und Probleme lösen“. Insbesondere können sie sich im Mathematikunterricht in ihrem Handeln als selbstwirksam erleben. - Berufliche Orientierung (BO)
Während der Entwicklung ihrer mathematischen Fähigkeiten erkennen die Schülerinnen und Schüler auch ihre Interessen und Potenziale im mathematisch-naturwissenschaftlichen Bereich und werden in der Erkenntnis gefördert, dass es hier keine geschlechtsspezifischen Unterschiede zu geben braucht. In geeigneten Aufgabenzusammenhängen erleben sie die Bedeutung der Mathematik in verschiedenen Berufen. Dies trägt zur Fähigkeit für selbstbestimmte und kompetente Entscheidungen bei der Auswahl aus dem Angebot der Arbeitswelt bei. - Medienbildung (MB)
Informationen sind in den Medien häufig in Form von Statistiken – insbesondere durch graphisch aufbereitete Darstellungen – gegeben. Es gehört zu den Aufgaben der Medienbildung, die Schülerinnen und Schüler zu befähigen, solche Informationen zu beschaffen, die Quellen zu prüfen und die Darstellungen kritisch zu interpretieren. Bei der mathematischen Verarbeitung und der medialen Aufbereitung eigener statistischer Erhebungen werden digitale Hilfsmittel – Rechner oder Software – eingesetzt, deren Nutzung die Schülerinnen und Schüler dabei erlernen oder vertiefen. Digitale Hilfsmittel, zum Beispiel Tabellenkalkulationssoftware oder dynamische Geometriesoftware, unterstützen den mathematischen Lernprozess, indem durch sie anschaulich und ohne großen Zeitaufwand mathematisches Verständnis ausgebildet werden kann. Indem die Schülerinnen und Schüler ihre Überlegungen, Lösungswege, Begründungen und Ergebnisse medial aufbereiten, trainieren sie sowohl die Ausdrucksfähigkeit in der Fachsprache als auch das Verfassen verständlicher Darstellungen bei geeignetem Medieneinsatz. Von allen Leitperspektiven nimmt daher die Medienbildung im Rahmen des Mathematikunterrichts einen besonderen Platz ein. - Verbraucherbildung (VB)
Die Mathematik unterstützt mit ihren gedanklichen Werkzeugen ein selbstbestimmtes und verantwortungsbewusstes Verbraucherverhalten, indem sie ermöglicht, fundierte Aussagen zu treffen und zu sachlich begründeten Bewertungen zu kommen. Durch eine gut ausgebildete mathematische Kompetenz und Sensibilisierung für mathematische Zusammenhänge können die Schülerinnen und Schüler zum Beispiel pseudomathematische Argumentationen bei Angeboten durchschauen und werden besonders für die selbstständige Bewältigung ihrer finanziellen Angelegenheiten vorbereitet.
1.2 Kompetenzen
Die ständigen Veränderungen in der Gesellschaft fordern von ihren Mitgliedern dynamische und flexible Fähigkeiten, um aktiv teilhaben und mitwirken zu können. Die mathematischen Kompetenzen, die sie dazu befähigen, beziehen sich einerseits auf die Inhalte des Faches und andererseits auf die zentralen mathematischen Prozesse, wie zum Beispiel Problemlösen, Modellieren oder Argumentieren. Bei jedem konkreten mathematischen Arbeiten kommen beide zusammen: Eine erfolgreiche Anwendung von Kenntnissen zu mathematischen Inhalten geschieht immer in Zusammenhang mit mathematischen Prozessen.
Für eine verständliche und übersichtliche Darstellung sind die beiden Aspekte voneinander getrennt erläutert als
- prozessbezogene Kompetenzen,
- inhaltsbezogene Kompetenzen.
Ein kompetenzorientierter Unterricht berücksichtigt stets beide Aspekte durch eine enge Verbindung von inhaltsbezogenen und prozessbezogenen Kompetenzen.
Bei den Festlegungen zu diesen mathematischen Kompetenzen folgen die hier vorgelegten Standards den Vorgaben der Kultusministerkonferenz (KMK). Wo sich innerhalb der Leitideen tiefergehende Möglichkeiten zur Verschränkung der beiden Kompetenzarten anbieten, wird auf prozessbezogene Kompetenzen verwiesen.
Der Zusammenhang zwischen Kompetenzen und Anforderungsbereichen
Sowohl die inhaltsbezogenen als auch die prozessbezogenen Kompetenzen können in unterschiedlichen Anforderungsbereichen erworben werden. Die Charakterisierung der drei Anforderungsbereiche kann vereinfachend beschrieben werden durch Reproduzieren (I), Zusammenhänge herstellen (II) und Verallgemeinern und Reflektieren (III).
Die folgende graphische Darstellung soll veranschaulichen, wie man mathematische Tätigkeiten in den Dimensionen Inhalte, Prozesse und Anforderungsbereiche verorten kann. Eine konkrete mathematische Tätigkeit verbindet immer inhaltsbezogene und prozessbezogene Kompetenzen (möglicherweise auch mehrere untereinander) und kann dabei einen oder mehrere Anforderungsbereiche einbeziehen:
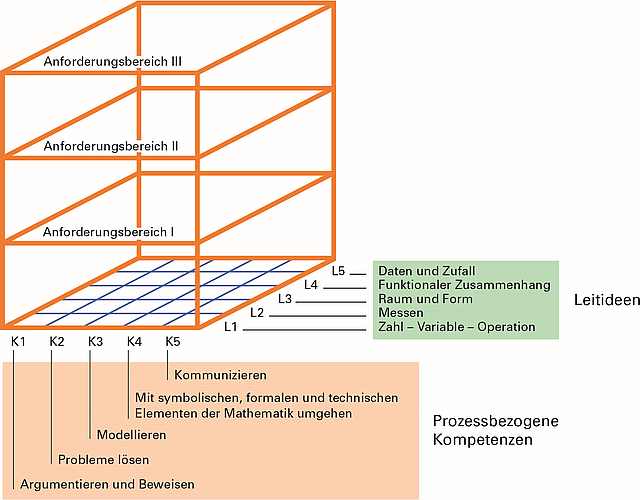 |
Prozessbezogene Kompetenzen
Diese sind gegliedert in die fünf Bereiche
- Argumentieren und Beweisen,
- Probleme lösen,
- Modellieren,
- Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen,
- Kommunizieren.
Diese übergreifenden Kompetenzen beziehen sich auf typische mathematische Tätigkeiten über alle mathematischen Inhalte hinweg und sollen sich im Bildungsprozess bis zum Ende des Bildungsgangs bei allen Schülerinnen und Schülern herausbilden. Sie werden weder nach Niveau noch nach Klassenstufen differenziert dargestellt. In wenigen Ausnahmefällen gibt es allerdings durch (E) gekennzeichnete Beschreibungen, die nur für das erweiterte Niveau (E) gelten (siehe Ausführungen zu den Leitideen).
Die Ausführungen zu den einzelnen Kompetenzen sind – soweit es möglich und sinnvoll erscheint – sehr konkret, um die anzustrebenden Fähigkeiten für das unterrichtliche Arbeiten präzise, umfassend und eindeutig zu beschreiben.
Die verständnisorientierte Auseinandersetzung mit mathematischen Inhalten sowie die Anwendungsorientierung im Unterricht ermöglichen forschendes Lernen und Entdecken von mathematischen Zusammenhängen. Inner- und außermathematische Problemstellungen werden im Unterricht vernetzt und haben das Entwickeln und Nachvollziehen von Problemlösungen sowie das Reflektieren von Strategien zum Ziel. Die Schülerinnen und Schüler lernen dabei, mathematisch zu denken, zu kommunizieren, zu argumentieren und zu begründen. Vermutungen äußern, Fragen stellen, recherchieren und Informationen auf Relevanz untersuchen, Lösungen dokumentieren, überprüfen und präsentieren sowie der konstruktive Umgang mit Fehlern und Kritik sind Ziele und Bestandteile des Mathematikunterrichts.
Leitideen
Die Leitideen sind gegliedert in die fünf Bereiche
- Zahl – Variable – Operation,
- Messen,
- Raum und Form,
- Funktionaler Zusammenhang,
- Daten und Zufall.
Diese Leitideen spiegeln die zentralen Ideen des Faches Mathematik wider, wie sie sich in der Entwicklung herauskristallisiert haben. Ausgehend von konkreten, im Alltag verhafteten Konzepten, wie dem der Zahl und des Messens einerseits und der Entwicklung zunehmend abstrakter geometrischer Konzepte zur Erfassung von Raum und Form andererseits, wurden in der Geschichte der Mathematik Ideen wie Approximation und Algorithmus entwickelt. Dabei spielten die Herausforderungen durch Naturwissenschaft und Technik eine zentrale Rolle, was in der Mathematik sowohl das Denken in funktionalen Zusammenhängen als auch Ideen für den Umgang mit großen Datenmengen und zufälligen Erscheinungen angeregt hat.
Die Leitideen beschreiben eine übergreifende Perspektive auf mathematische Inhalte. Daher stellen sie auch keine zeitliche Strukturierung für den Unterricht dar, sondern sollen spiralig und vernetzend immer wieder aufgegriffen und in ihrer übergreifenden Bedeutung deutlich werden.
Insbesondere können sich inhaltsbezogene Kompetenzen auch auf verschiedene Leitideen beziehen und Leitideen über bestimmte Inhalte miteinander verbunden sein. In diesen Standards beschreibt zum Beispiel die Leitidee Messen vor allem das Grundprinzip des Messens und die Wege zur Bestimmung von Flächen- oder Rauminhalten, während die zu messenden Größen selbst (wie Abstände, Winkel) der Leitidee Raum und Form zuzurechnen sind. Entsprechende Berührungspunkte gibt es zwischen den Leitideen Zahl – Variable – Operation und Funktionaler Zusammenhang. Verweise zwischen den Leitideen dienen hier der Klarstellung und unterstützen den Gedanken der Vernetzung.
Kursivsetzung von Begriffen in den Leitideen
Fachbegriffe, die kursiv geschrieben sind, sind im Unterricht verbindlich mit dem Ziel einzusetzen, dass die Schülerinnen und Schüler diese
- in unterschiedlichen Kontexten ohne zusätzliche Erläuterung verstehen und anwenden können,
- im eigenen Wortschatz als Fachsprache aktiv benutzen können,
- mit eigenen Worten korrekt beschreiben können.
Fachbegriffe, die in den Standards nicht kursiv gesetzt sind, werden verwendet, um die Kompetenzbeschreibung für die Lehrkräfte fachlich präzise und prägnant formulieren zu können. Die Schülerinnen und Schüler müssen über diese Fachbegriffe nicht verfügen können.
Formeln sind verbindlich im Unterricht so zu behandeln, dass die Schülerinnen und Schüler am Ende des Kompetenzerwerbs diese kennen, ihre inhaltliche Bedeutung wiedergeben und sie anwenden können.
Bezug zwischen prozessbezogenen Kompetenzen und inhaltsbezogenen Kompetenzen
Die einzelnen Kompetenzbeschreibungen legen sowohl die konkreten Inhalte als auch die damit verbundenen Fähigkeiten präzise und eindeutig fest. Grundsätzlich können zusammen mit jeder inhaltsbezogenen Kompetenz prozessbezogene Kompetenzen gefördert werden. Wo jedoch bei einer Teilkompetenz in einer Leitidee ein expliziter Verweis auf prozessbezogene Kompetenzen steht, soll dies als Hinweis darauf verstanden werden, dass diese prozessbezogene Kompetenz an dieser Stelle in besonders geeigneter Weise aufgegriffen werden kann. Wegen des eher exemplarischen Gebrauchs solcher Verweise ist das ständige Bewusstsein umso wichtiger, dass Mathematikunterricht erst in der Verzahnung von Inhalten und Prozessen lebendig werden kann.
Klassenstufen und Niveaustufen
Die Leitideen für die Klassenstufen 7, 8, 9 enthalten auch Kompetenzen, die für den Hauptschulabschluss nicht verlangt werden, dies erkennt man am Zusatz [MSA] bei der Teilkompetenznummer, zum Beispiel (4)[MSA]. Durch diese Kennzeichnung wird auch deutlich, dass Schülerinnen und Schüler, die einen mittleren Schulabschluss auf der Niveaustufe G anstreben, einen Teil der zugehörigen Kompetenzen schon im Verlauf der Klasse 9 erwerben müssen.
Die Standards definieren im G–Niveau die Kompetenzen für den Hauptschulabschluss (ohne die durch [MSA] gekennzeichneten Teilkompetenzen), für einen mittleren Schulabschluss in der Werkrealschule (mit den durch [MSA] gekennzeichneten Teilkompetenzen), und im M–Niveau für einen Realschulabschluss.
1.3 Didaktische Hinweise
Um sowohl prozessbezogene als auch inhaltsbezogene mathematische Kompetenzen zu entwickeln, benötigen Schülerinnen und Schüler aktive Aneignungsprozesse und -handlungen, in denen sie Mathematik betreiben und neu gewonnene Erkenntnisse zu bereits vorhandenen Vorstellungen in Beziehung setzen.
Nachhaltigkeit und Vernetzung von Wissen
Die Leitideen ermöglichen die Formulierung eines Curriculums, welches Grundbegriffe auf verschiedenen kognitiven und sprachlichen Niveaus bis hin zu abstrakten formalisierten Darstellungen immer wieder aufgreift und spiralcurricular weiterentwickelt. Den Schülerinnen und Schülern wird dadurch die Möglichkeit gegeben, fachlichen Gegenständen propädeutisch zu begegnen, sie wiederaufzunehmen und zu vertiefen. Diese Phasen immer wiederkehrender Auseinandersetzung mit Inhalten führen zu einer zeitlichen Streckung des Lernprozesses und zu einem vertieften, auf Nachhaltigkeit ausgelegten Kompetenzaufbau. Im Unterricht stehen die fünf Leitideen nicht isoliert nebeneinander; Beziehungen und Sinnzusammenhänge, auf die in den Bildungsstandards in Form von Querverweisen hingewiesen wird, führen zu einer Vernetzung des Wissens und der Inhalte, so dass ein integriertes Verständnis von Mathematik entsteht.
Grundvorstellungen und Lernprozesse
Damit die Lernenden Mathematik sinnerfüllt erleben und verstehen, müssen die schon in der Grundschule angebahnten Grundvorstellungen tragfähig weiterentwickelt, ergänzt und im Bedarfsfall revidiert werden. Die Grundvorstellungen ermöglichen den Schülerinnen und Schülern, einen Sinnzusammenhang zwischen der mathematischen und der realen Welt herzustellen: Ein mathematisches Konzept kann erst sinnvoll eingesetzt werden, wenn die entsprechenden Grundvorstellungen dazu aktiviert werden können (zum Beispiel benötigt das Addieren von Brüchen Grundvorstellungen zu Brüchen als Anteil und zur Verfeinerung von Anteilsdarstellungen). Grundvorstellungen bilden so die notwendige Basis für mathematisches Verständnis und damit für den Aufbau mathematischer Kompetenzen. Stabile Grundvorstellungen sind Voraussetzung dafür, auch auf längerfristig zurückliegende mathematische Begriffe und Regeln nachhaltig zugreifen zu können.
Das Lernen von Mathematik ist ein konstruierend-entdeckender Prozess, der sich an bereits vorhandene Kompetenzen anschließt und in dessen Verlauf man zur Auseinandersetzung mit mathematischen Sachverhalten angeregt wird. Methodisch kann dies in unterschiedlichen Lernumgebungen durch individuelle oder kooperativ gestaltete Arbeitsphasen wie auch in Plenumsphasen erreicht werden. Unabhängig von der Methode sind klar vorgegebene Strukturen und wohlüberlegte Instruktion durch die Lehrkraft Grundvoraussetzungen für den Unterrichtserfolg.
Guter Mathematikunterricht bedarf kognitiv aktivierender, reichhaltiger, möglichst authentischer und motivierender inner- und außermathematischer Problemsituationen, die das Potenzial beinhalten, Begriffe, Regeln, Lösungsverfahren oder Modellierungen entweder selbstständig zu entdecken oder begründet zu konstruieren. Dabei spielen die eigenständige Bearbeitung von Frage- und Problemstellungen, die Reaktivierung des Vorwissens, die Auseinandersetzung mit unterschiedlichen Zugangs- und Lösungsmöglichkeiten, ein konstruktiver Umgang mit Fehlern und die Möglichkeit zur Kooperation zwischen den Lernenden eine wichtige Rolle. Vorgegebene Darstellungen zu interpretieren und zu bewerten, eigene Darstellungen zu entwickeln und zwischen verschiedenen Darstellungsebenen zu wechseln trägt zur Entwicklung und Vertiefung von mathematischem Verständnis bei.
Üben und Aufgabenauswahl
Dem Üben kommt im Mathematikunterricht eine wichtige Rolle zu.
Einerseits beinhaltet es operatives und kognitiv anregendes Üben, mit dem die Beweglichkeit des Denkens gefördert und starren, einseitigen Schemata entgegengewirkt werden soll. Dazu bedarf es einer hinreichenden Variation an Aufgabenformaten (Umkehren, Analogisieren, Verallgemeinern, …). In Übungsphasen kann es durch die Wahl geeigneter Aufgabenstellungen möglich sein, weiterführende mathematische Strukturen und Zusammenhänge von den Schülerinnen und Schülern entdecken zu lassen (produktives Üben).
Andererseits soll auch das Beherrschen von mathematischen Verfahren und Kalkülen durch Üben so ausgebildet werden, dass grundlegende Algorithmen sicher ausgeführt werden können. Bei komplexeren Aufgabenstellungen, etwa beim Problemlösen und Modellieren, kommt dieser Fertigkeit eine wichtige Entlastungsfunktion zu. Im Rahmen der Automatisierung mathematischer Fertigkeiten ist jedoch auf vielfältige Reflexionen über die eigene Vorgehensweise zu achten.
Übungsphasen beschränken sich nicht allein auf Übungsstunden, sondern sind Bestandteil einer jeden Mathematikstunde. Auch in Erarbeitungsphasen werden aktuelle Unterrichtsinhalte mit vergangenen vernetzt, die durch wiederholendes Üben aktiviert werden, so dass ein sinnvolles Weiterlernen ermöglicht wird.
Innermathematische beziehungsweise anwendungsbezogene Fragestellungen fördern neben dem Erwerb inhaltlicher Kompetenzen die Ausbildung prozessbezogener Kompetenzen und ermöglichen einen Bezug zu den Leitperspektiven.
Heterogenität der Schülerinnen und Schüler
Die Heterogenität der Schülerinnen und Schüler erfordert einerseits von Lehrerseite binnendifferenzierende Maßnahmen, wie zum Beispiel paralleldifferenzierte, stufendifferenzierte oder selbstdifferenzierende Aufgaben, Differenzierung bei den Zugangsweisen oder individualisierende Unterrichtsformate mit dem Ziel, den individuellen Lernvoraussetzungen gerecht zu werden und der Individualität der Schülerinnen und Schüler Entfaltungsmöglichkeiten zu geben. Sie bietet den Schülerinnen und Schülern andererseits die Möglichkeit, auf Basis unterschiedlicher Erfahrungshintergründe, Arbeits- und Herangehensweisen miteinander in einen Dialog über unterschiedliche Sichtweisen zu treten, sich gegenseitig Impulse zu geben und so personale und soziale Kompetenzen weiterzuentwickeln.
Der Diagnose mathematischer Kompetenzen und den sich daran anschließenden gezielten Fördermaßnahmen kommt in einem Heterogenität berücksichtigenden Unterricht große Bedeutung zu.
Hilfsmittel didaktisch nutzen
Mediale Hilfsmittel stellen einerseits bei der Ausbildung von Grundvorstellungen eine notwendige Unterstützung dar, andererseits bereitet der Umgang mit ihnen die Schülerinnen und Schüler auf eine zunehmend technisierte und digitalisierte Lebens- und spätere Berufswelt vor.
Geeignete Hilfsmittel ermöglichen insbesondere didaktisch sinnvolle Zugänge zu neuen Inhalten und können zu vertiefter und nachhaltiger Entwicklung von mathematischem Denken beitragen. Sie erlauben den Schülerinnen und Schülern vielfältige und individuelle Möglichkeiten des heuristischen und experimentellen Arbeitens und entlasten bei Problemlöseprozessen von algorithmischen und kalkülhaften Tätigkeiten.
